本文最后更新于 2025-03-17T10:30:11+08:00
基本概念
归结算法 归结反演: steps:
将α取否定,放到KB中
将更新的KB转换为clausal form得到新的子句集S
反复调用单步归结
如果得到空子句,即S|- (),说明KB ∧¬α 不可满足,算法终止,可得KB |= α
如果一直归结直到不产生新的子句,在这个过程中没有得到空子句,则KB |= α不成立
clausal form–便于计算机处理的形式
每一个子句对应一个元组 ,元组中的每一个元素是一个原子公式或原子公式的否定,元素之间的关系是析取关系 ,表示只要一个原子成立,即子句成立。
ps:元组是用逗号 分隔的,即使只有一个元素,也需要在元素后面加上逗号 ,以区分它与普通变量的不同
元组的集合组合子句集S,子句集中的每个句子之间是合取关系
单步归结:
从两个子句中分贝寻找相同的原子及其对应的原子否定(只能找其中一组,如果出现两组互补对不可以同时归结)
去掉该互补对,并将剩余元素合并为新子句
举例:
最一般合一算法 合一
通过变量替换 使得两个子句能够被归结(有相同的原子),所以合一也被定义为使得两个原子公式等价的一组变量替换/赋值
由于一阶逻辑中存在变量,所以归结之前需要进行合一,如(P(john),Q(fred),R(x))和(¬P(y),R(susan),R(y))两个子句中,我们无法找到一样的原子及其对应的否定,但是不代表它们不能够归结
通过将y替换为john(替换一定要全部替换 ),我们得到了(P(john),Q(fred),R(x))和(¬P(john),R(susan),R(john)),此时我们两个子句分别存在原子P(john)和它的否定¬P(john),可以进行归结
最一般合一 指使得两个原子公式等价,最简单的一组变量替换
输入:两个原子公式,它们有相同的谓词,不同的参数项和‘’¬“
输出:一组变量替换/赋值
流程:
Tips:变量替换是从两个原子公式中找到的,但是最后要施加给整个子句的
一阶逻辑归结算法:
要求 存储公式 的python数据结构
用字符串存储
符号¬用‘~’代替
谓词 的首字母大写 , 例如用A, B, C, P1, P2, Student等表示; 谓词的每个参数之间用逗号“,”间隔且不加空格
常量 用小写单词或a, b, c等小写字母表示;
本次作业的公式中不含∃,∀量词符号
例子: ¬child存储为 “~child” boy存储为“boy”
几个公式: “R(a)”, “~P(a,zz)”, “Student(tony)”. 这里应该将a,tony看做常量,将zz看做变量
存储子句 的python数据结构
用tuple的方式存储
例子:
¬child˅¬male˅boy存储为(‘child’, ‘male’, ‘boy’)
¬S(z) ˅ L(z, snow)存储为(‘~S(z)’, ‘L(z,snow)’)
存储子句集 的python数据结构
实现过程 实验一:命题逻辑的归结推理 内容: 编写函数ResolutionProp实现命题逻辑的归结推理,函数要点如下:
输入为子句集, 每个子句中的元素是原子命题或其否定.
输出归结推理的过程, 每个归结步骤存为字符串 , 将所有归结步骤按序存到一个列表中并返回, 即返回的数据类型为 list[str].
一个归结步骤的格式为 步骤编号 R[用到的子句编号] = 子句. 如果一个字句包含多个公式,则每个公式用编号 a,b,c...区分,如果一个字句仅包含一个公式,则不用编号区分.(见课件和例题)
例子: 输入子句集
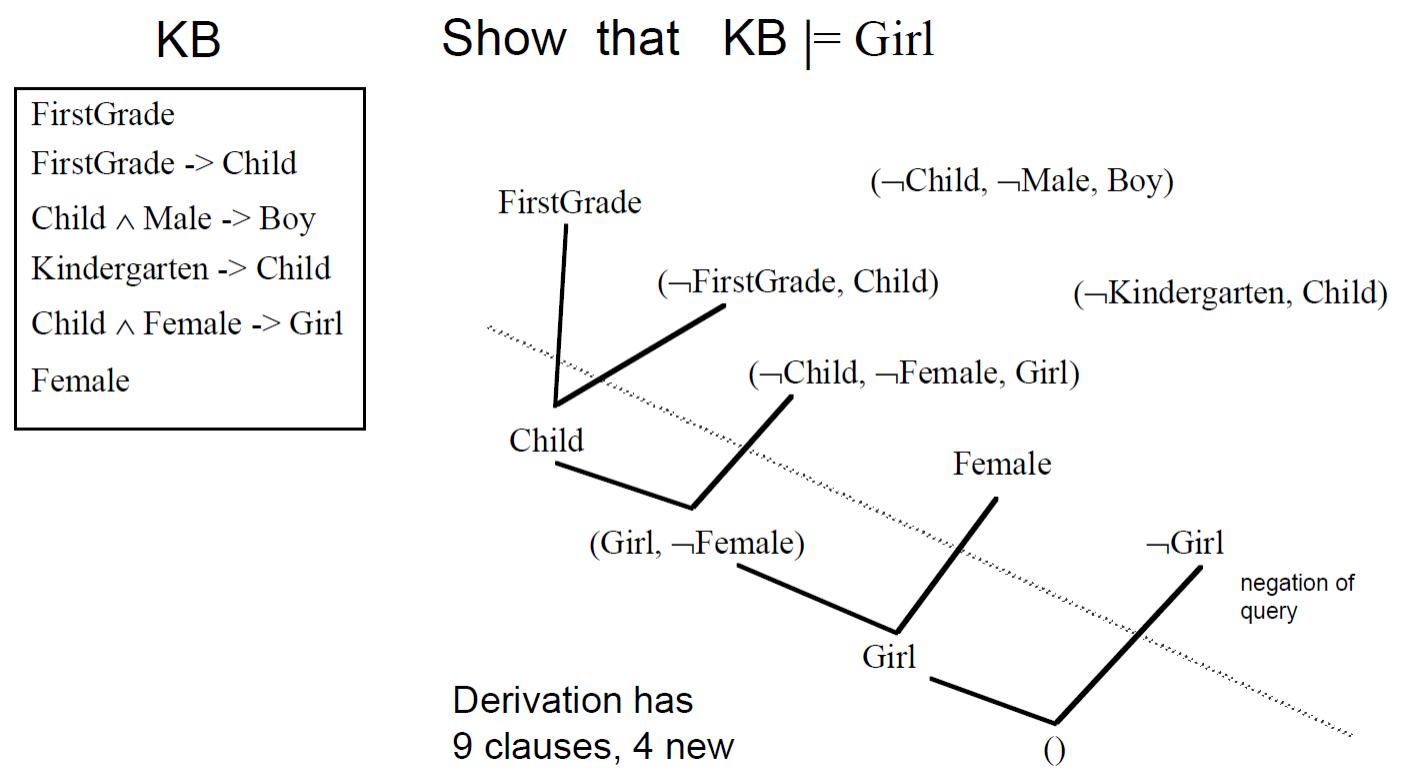
1 KB = {(FirstGrade,), (~FirstGrade,Child), (~Child,)}
则调用 ResolutionProp(KB)后返回推理过程的列表如下:
1 2 3 4 5 1 (FirstGrade,),2 (~FirstGrade,Child)3 (~Child,),4 R[1 ,2 a] = (Child,),5 R[3 ,4 ] = ()
ResolutionProp()函数working on…
这里我们设置了两个字典用于存储子句的编号以及子句中元素的编号,方便后续打印;同时先将基本的子句集列举出来
设置processed_KB用于记录已经归结过的子句,同时建立一个new_KB用于记录每轮新增子句,原KB用于不断更新–保存旧子句和加入新子句
在进行归结时,需要将完整子句集与新增子句集进行归结,进行归结的子句需要没被归结过–也就是不在processed_KB之中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 def ResolutionProp (KB ):1 for clause in KB:f"{k} {clause} " )if len (clause) > 1 : chr (97 + i) for i, ele in enumerate (clause)} 1 list (KB)set () set (clauses) while new_KB:list (new_KB) for i in range (len (current_clauses)):for j in range (len (clauses)): if current_clauses[i] == clauses[j]: continue if current_clauses[i] in processed_KB : continue if clauses[j] in processed_KB :continue if res is not None :str (clause_dict[current_clauses[i]])str (clause_dict[clauses[j]])if len (current_clauses[i]) > 1 and resolved_literals[0 ] in clause_labels[current_clauses[i]]:0 ]]if len (clauses[j]) > 1 and resolved_literals[1 ] in clause_labels[clauses[j]]:1 ]]if res == ():f"{k} R[{clause1_id} ,{clause2_id} ] = ()" )return stepsif res not in clause_dict:if len (res) > 1 :chr (97 + i) for i, lit in enumerate (res)}f"{k} R[{clause1_id} ,{clause2_id} ] = {res} " )1 return steps
resolve()函数!这个函数主要用于做单步归结 !
思路:
遍历子句1中的所有元素,对每一个元素都取反,查看这个取反的元素是否在子句2中,如果存在,说明找到了一组互补对,进行归结,并返回新的子句集(合并并去掉互补对)以及互补对;如果取反的元素不在子句2中继续遍历。
如果遍历到结尾都没有找到,说明这两句无法进行归结,返回空。
1 2 3 4 5 6 7 8 9 10 11 12 def resolve (clause1, clause2 ):for literal in clause1:f"~{literal} " if literal[0 ] != '~' else literal[1 :]if complement in clause2:tuple (sorted (set (clause1).union(set (clause2)) - {literal, complement}))if not new_clause:return (), (literal, complement)return new_clause, (literal, complement)return None , None
其他注意点:
子句是元组,但由于元组是一种不可修改的数据结构,我们需要在合并子句集的时候就去除互补对。
main函数main函数比较简单,只需要设置好子句集,然后调用ResolutionProp函数,再输出steps这个字符串列表就好了。可以增加一些新例子。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 def main ():'FirstGrade' ,), '~FirstGrade' , 'Child' ), '~Child' ,)'a' ,),'b' ,)'A' ,), '~A' , 'B' ), '~B' ,)'P' , 'Q' ), '~P' , 'R' ), '~Q' , 'R' ), '~R' ,)'A' , 'B' ), '~A' , 'C' ), '~B' , 'D' ), '~C' , '~D' )for step in steps:print (step)
实验二:最一般合一算法 编写函数 MGU实现最一般合一算法. 该函数要点如下:
输入为两个原子公式 , 它们的谓词相同 . 其数据类型为 str, 格式详见课件.
输出最一般合一的结果, 数据类型为 dict, 格式形如**{变量: 项, 变量: 项}**, 其中的变量和项均为字符串.
若不存在合一, 则返回空字典.
例子:
调用 MGU('P(xx,a)', 'P(b,yy)')后返回字典 {'xx':'b', 'yy':'a'}.
调用 MGU('P(a,xx,f(g(yy)))', 'P(zz,f(zz),f(uu))')后返回字典 {'zz':'a', 'xx':'f(a)', 'uu':'g(yy)'}.
提示
只含一个元素的 tuple类型要在末尾加 ,. 例如 ('a')是错误的写法, 而正确的写法是 ('a',).
{}会被解释成空字典. 若要定义空集合请用 set().
这一部分只写了一个函数(MGU)和一个辅助函数(用于判断是否含有变量)
MGU(literal1,literal2) 实现思路:
输入:两个谓词相同的原子公式(字符串类型);
返回/输出:字典,格式:{变量: 项, 变量: 项}
首先处理原子公式,我们需要对各个位置的变量or项进行比较,在此之前,我们可以去掉谓词P(),然后再使用分词器split来将字符串分割成列表元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 for i in range (len (literal1)):if literal1[i]!='(' :1 else :break 1 :-1 ].split(',' )1 :-1 ].split(',' )if len (lit1)!=len (lit2):return None
最重要的处理部分–主要思想就是一个个元素比较,分三类 :
两个元素都是变量–无法合一,返回None
一个元素是变量,另一个是项–用项替代变量,并加入到res字典中,同时把式子中所有相同变量用项替代
两个元素都是项–分析是不是f()或f(g())这种函数嵌套的项,如果都含有f(),需要进行递归 判断(递归调用MGU() )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 for i in range (len (lit1)):if lit1[i]==lit2[i]:continue if lit1[i] != lit2[i]:if v1 and v2:return None elif v1 is True and v2 is False :if v1 in res:return None for j in range (i+1 ,len (lit1)):elif v2 is True and v1 is False :if v2 in res:return None for j in range (i+1 ,len (lit1)):else :if '(' in lit1[i] and '(' in lit2[i]:if sub_res is None :return None else : else : return None
Check_Var() 很普通的一个函数,这里我只判断了是否存在x,y,z,u这几个变量,如果有更多函数符号可以添加,或者后面修改成传递变量集(but…lazy)
简单测试一下: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def main ():'P(a,xx,f(g(yy)))' 'P(zz,f(zz),f(uu))' if res is not None :for key,value in res.items():print (key,":" ,value)else :print ("NO MGU found" )
输出:
1 2 3 zz : a xx : f (a )uu : g (yy )
一阶逻辑的归结推理 编写函数 ResolutionFOL实现一阶逻辑的归结推理. 该函数要点如下:
输入为子句集, KB子句中的每个元素是一阶逻辑公式 (不含全称量词和存在量词等量词符号)
输出归结推理的过程, 每个归结步骤存为字符串, 将所有归结步骤按序存到一个列表中并返回, 即返回的数据类型 为 list[str]
一个归结步骤的格式为 步骤编号 R[用到的子句编号]{最一般合一} = 子句, 其中最一般合一输出格式为”{变量=常量, 变量=常量}”.如果一个字句包含多个公式,则每个公式用编号 a,b,c...区分,如果一个字句仅包含一个公式,则不用编号区分。
例题: 输入
1 KB = {(GradStudent (sue),),(~GradStudent (x ),Student (x)),(~Student (x),HardWorker (x)),(~HardWorker (sue),)}
则调用 ResolutionFOL(KB)后返回推理过程的列表如下:
1 2 3 4 5 6 7 1 (GradStudent(sue),)2 (~GradStudent(x),Student(x))3 (~Student(x),HardWorker(x))4 (~HardWorker(sue),)5 R[1 ,2 a]{x=sue} = (Student(sue),)6 R[3 a,5 ]{x=sue} = (HardWorker(sue),)7 R[4 ,6 ] = []
输入
1 KB = {(A (tony),),(A (mike),),(A (john),),(L (tony,rain),),(L (tony,snow),),(~A (x ),S (x),C (x)),(~C (y),~L (y,rain)),(L (z,snow),~S (z)),(~L (tony,u),~L (mike,u)),(L (tony,v),L (mike,v)),(~A (w),~C (w),S (w))}
输出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 (A(tony),)2 (A(mike),)3 (A(john),)4 (L(tony,rain),)5 (L(tony,snow),)6 (~A(x),S(x),C(x))7 (~C(y),~L(y,rain))8 (L(z,snow),~S(z))9 (~L(tony,u),~L(mike,u))10 (L(tony,v),L(mike,v))11 (~A(w),~C(w),S(w))12 R[2 ,11 a]{w=mike} = (S(mike),~C(mike))13 R[5 ,9 a]{u=snow} = (~L(mike,snow),)14 R[6 c,12 b]{x=mike} = (S(mike),~A(mike),S(mike))15 R[2 ,14 b] = (S(mike),)16 R[8 b,15 ]{z=mike} = (L(mike,snow),)17 R[13 ,16 ] = []
输入
1 KB = { ( On ( tony , mike ) , ) , ( On ( mike , john ) , ) , ( Green ( tony ) , ) , ( ~ Green ( john ) , ) , ( ~ On ( xx , yy ) ,~ Green ( xx ) , Green ( yy ) ) }
输出
1 2 3 4 5 6 7 8 9 10 1 (On (tony,mike),),2 (On (mike,john),),3 (Green(tony),),4 (~Green(john),),5 (~On (xx,yy),~Green(xx),Green(yy)),6 R[4 ,5 c]{yy=john} = (~On (xx,john),~Green(xx)),7 R[3 ,5 b]{xx=tony} = (~On (tony,yy),Green(yy)),8 R[2 ,6 a]{xx=mike} = (~Green(mike),),9 R[1 ,7 a]{yy=mike} = (Green(mike),),10 R[8 ,9 ] = ()
注意
只含一个元素的 tuple类型要在末尾加 ,. 例如 ('x')是错误的写法, 而正确的写法是 ('x',).
{}会被解释成空字典. 若要定义空集合请用 set().请提交代码时只提交一个 .py代码文件, 请不要提交其他文件.
例题和作业都会进行代码测试.
上述作业的输出仅供参考。如果有不同的归结顺序,结果相同的情况,代码也算正确.
实现思路:
参考以及复用大部分前两个任务的代码来构建
ResolutionFOL():算法思路:
将KB库以子句集的方式传入到函数中进行归结处理
对子句集反复进行单步归结,同时使用MGU算法进行合一处理
具体:
同上面的归结算法,由于输出时需要有美观的编号,我们设置了两个记录字典–clause_dict和clause_labels,前者记录子句的编号,后者记录子句中元素的编号(有多个元素的子句才需要)
类似地,先将子句集的子句进行编号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 k = 1 for clause in KB:f"{k} {clause_str} " )if len (clause) > 1 :for i, literal in enumerate (clause):chr (97 + i) 1
进入归结的主要步骤,需要维持一个已经归结的子句对的集合–保证子句对不会重复归结(这部分和上面的归结算法有点出入,前者只需要保证我归结过的句子不用再出现就可以了),但是由于我们可以对谓词P(x)赋不同的值,所以可以对他赋值后产生的新子句再次归结。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 def ResolutionFOL (KB ):1 for clause in KB:f"{k} {clause_str} " )if len (clause) > 1 :for i, literal in enumerate (clause):chr (97 + i) 1 1 list (KB)set () while True :for i in range (len (clauses)):for j in range (i + 1 , len (clauses)):if clauses[i] == clauses[j]: continue if (c1, c2) in processed:continue for resolvent_info in resolvents:str (clause_dict[c1])str (clause_dict[c2])if len (c1) > 1 and lit1 in clause_labels.get(c1, {}):if len (c2) > 1 and lit2 in clause_labels.get(c2, {}):if resolvent == ():f"{k} R[{clause1_id} ,{clause2_id} ]{mgu_str} = ()" )return simplified_stepsif resolvent not in clause_dict:if len (resolvent) > 1 :for idx, lit in enumerate (resolvent):chr (97 + idx)f"{k} R[{clause1_id} ,{clause2_id} ]{mgu_str} = {resolvent_str} " )1 if not new_resolvents:return steps
用于从归结步骤中提取父子句编号,用于筛选出真正有用的归结步骤
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def extract_parents (step ):if "R[" not in step:return None , None "R[" ) + 2 :step.index("]" )]',' )int ('' .join(c for c in parents[0 ] if c.isdigit()))int ('' .join(c for c in parents[1 ] if c.isdigit()))'' .join(c for c in parents[0 ] if c.isalpha())'' .join(c for c in parents[1 ] if c.isalpha())return parent1, parent2, parent1_suffix, parent2_suffix
get_step_number(step)获取编号,把step的第一个标号提取出来
1 2 def get_step_number (step ): return int (step.split(' ' )[0 ])
Simplify (steps, original_size)简化归结过程–把又臭又长的过程删减成有用的过程
记录初始子句集(也就是KB库转换的最初的子句集)
同时建立一个存储有用子句的集合
在旧的step的基础上进行筛选,同时创建新的编号,创建num2idx字典,用于存储编号到索引的映射
为了简化过程,我们是从空子句开始回溯,找到能得到空子句的核心步骤。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 def Simplify (steps, original_size ): 0 :original_size] for i, step in enumerate (steps):1 ])] set () while number:0 ) if number0 in processed: continue if step_index >= original_size: if parent_info[0 ] is not None :0 ], parent_info[1 ]if num1 > original_size and num1 not in processed:if num2 > original_size and num2 not in processed:for i, step in enumerate (final_steps):1 for i in range (original_size, len (final_steps)):if parent_info[0 ] is not None :0 ], parent_info[1 ]2 ], parent_info[3 ]f"R[{old_num1} {suffix1} ,{old_num2} {suffix2} ]" f"R[{new_num1} {suffix1} ,{new_num2} {suffix2} ]" 1 if old_step_num != new_step_num:str (new_step_num) + final_steps[i][len (str (old_step_num)):]return final_steps