conda指令

• 创建python虚拟环境
  conda create -n py36 python=3.6.5
• 进入某个python虚拟环境
  conda activate xxx
• 在虚拟环境中安装
  conda install numpy或pip install numpy

Anaconda环境管理-CSDN博客

实验四

1. 实验目的
   （1）深入理解和掌握离散时间非周期信号的傅里叶变换及计算方法；
   （2）熟悉离散时间傅里叶变换的性质；
   （3）理解离散时间 LTI 系统的频域分析原理和方法，掌握离散时间 LTI 系统的频率响应求解方法，并能编程绘制相应的幅频、相频响应曲线。

2. 实验原理
   

python提供的 scipy.signal.freqz()函数可以近似求解离散时间傅里叶变换。
无穷级数求和：SymPy符号函数求和方法： sum() summation() gosper_sum()等函数都可以用于级数求和操作。
SymPy符号函数积分的方法：integrate()
通过numpy库和scipy库可以产生基本的信号，如阶跃信号、指数信号、脉冲信号等等，其中scipy.signal可用于计算信号的卷积
Signal processing (scipy.signal) — SciPy v1.15.2 Manual

3. 性质
   
   
   

4. 实验任务
   （1）编程计算双边指数衰减信号$𝑥[𝑛] = e^{−2|𝑛|}$的离散时间傅里叶变换，并验证其时域内插，即
   $$
   \begin{cases}
   \begin{split}
   x[n/k],n为k的整数倍\
   0, 其他n
   \end{split}
   \end{cases}
   $$
   的离散时间傅里叶变换，取𝑘 = 3。请分别绘制$𝑥[𝑛]$和$𝑥_{k}[𝑛]$的幅频曲线和相频曲线。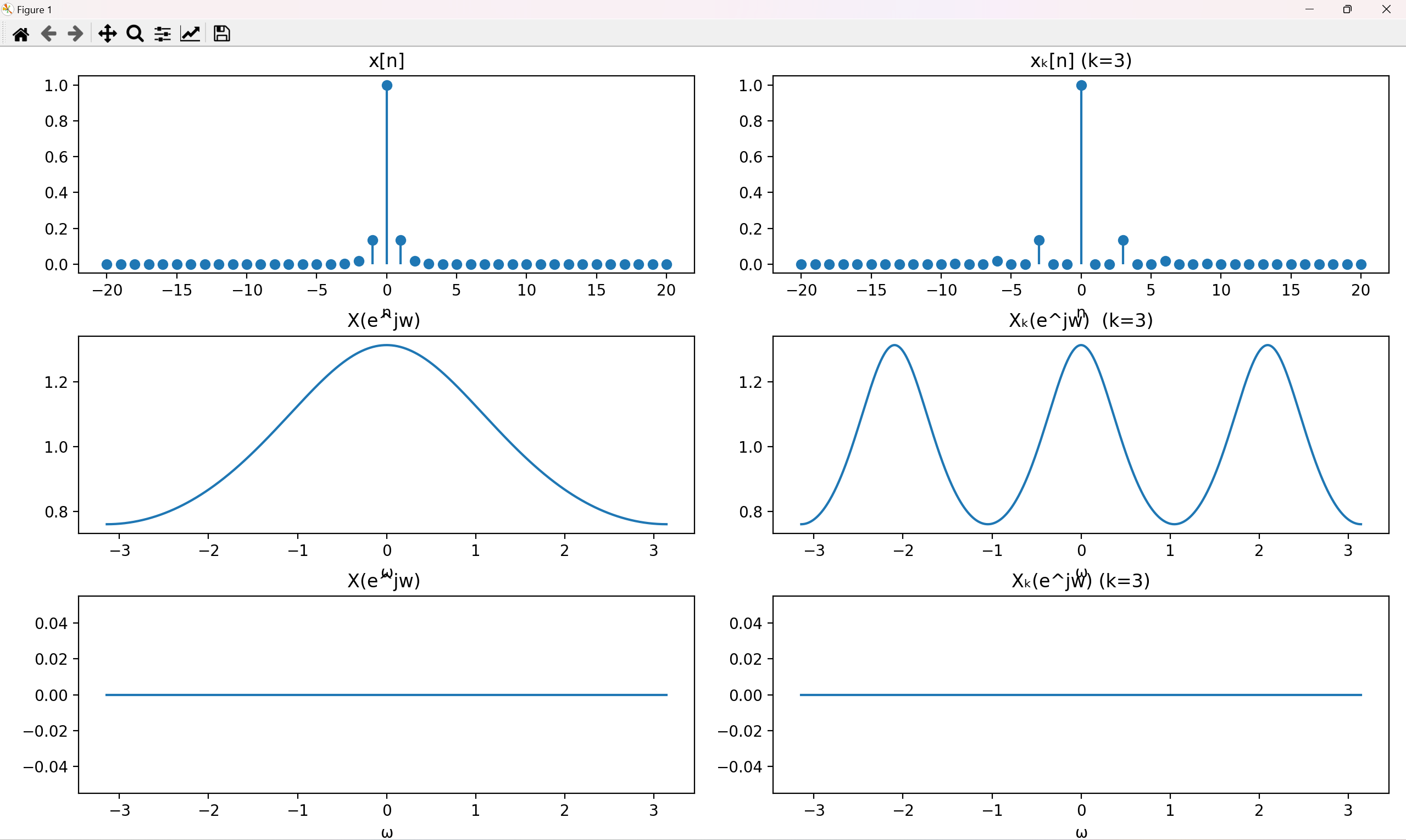
   

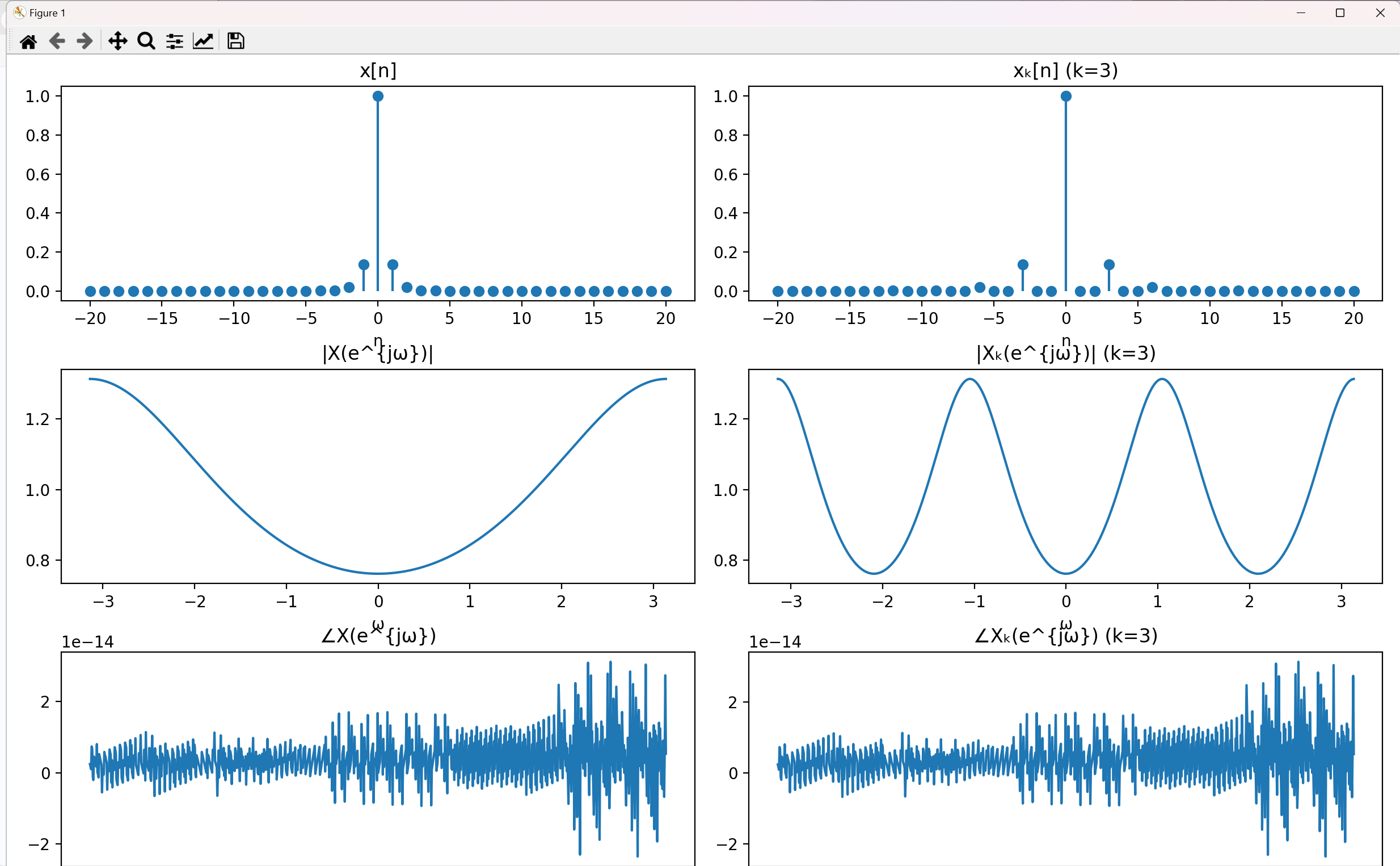
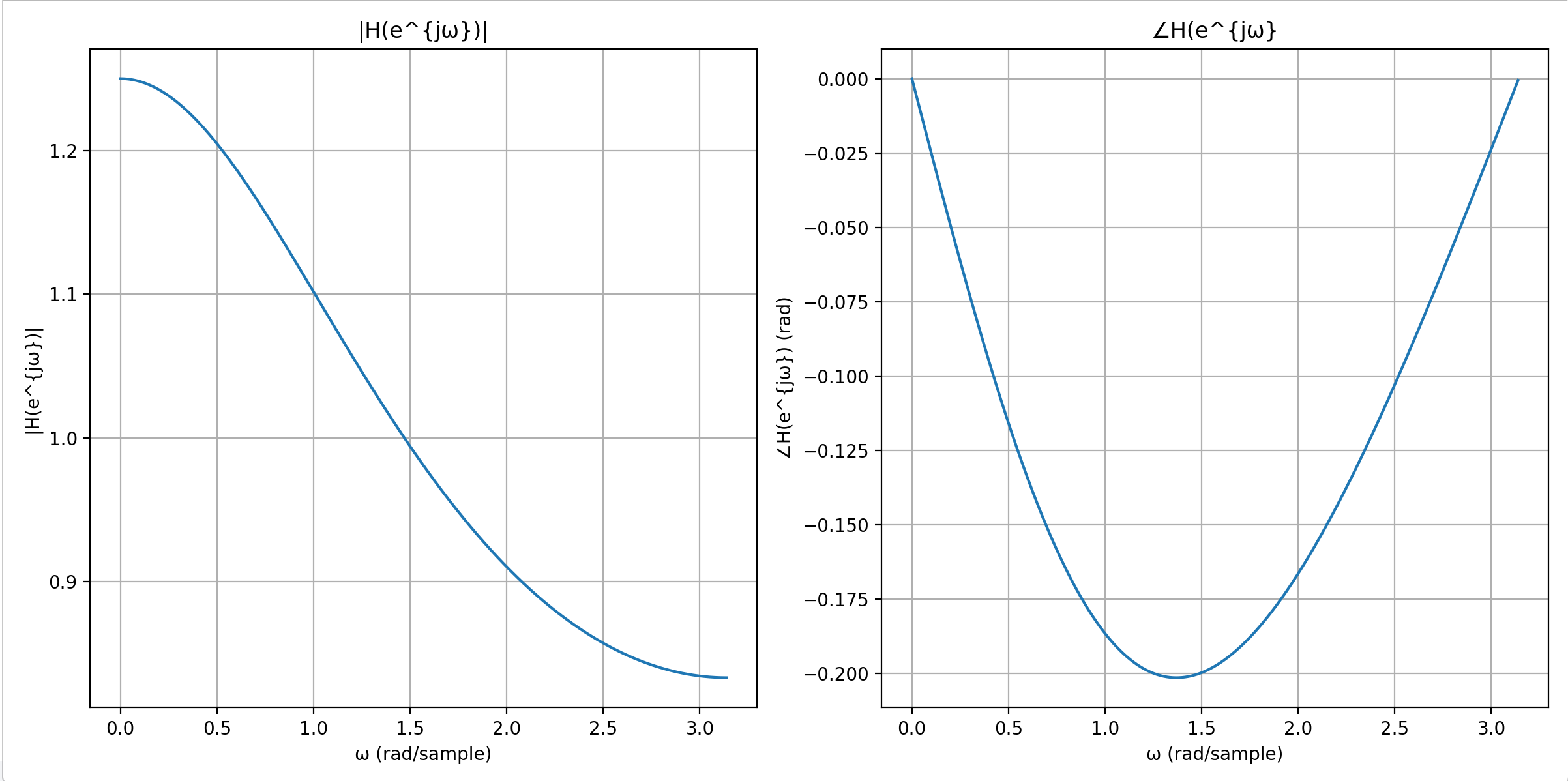
（2）考虑差分方程$𝑦[𝑛] − 𝑎𝑦[𝑛 − 1] = 𝑥[𝑛]$，其中|𝑎| < 1。取𝑎 =0.2，编程求解该方程所描述系统的频率响应，并：
（a）画出系统的幅频和相频特性曲线；
（b）求解系统的单位脉冲响应并绘制出图形

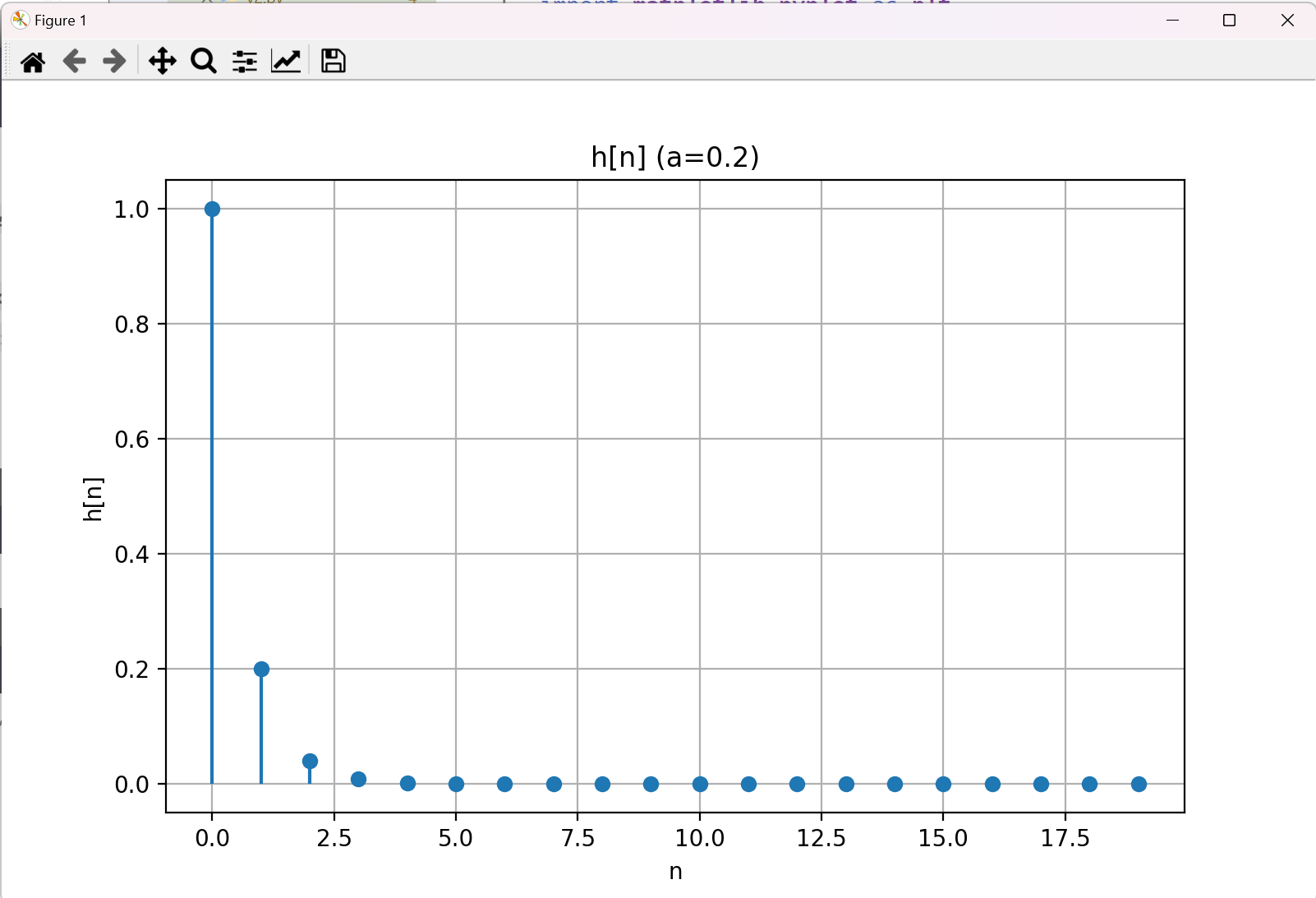
（3）设离散时间双边指数衰减信号$𝑥[𝑛] = e^{−2|𝑛|}, 𝑦[𝑛] = 𝑥[𝑛] ∗ 𝑥[𝑛]$，请
（a）编程用卷积性质求解$𝑌(e^{j𝜔})$与$𝑦[𝑛]$，并绘制$𝑥[𝑛]$、$|𝑌(e^{j𝜔})|$和$𝑦[𝑛]$的图像；
（b）编程用时域卷积求解$𝑦[𝑛]$，绘制$𝑦[𝑛]$的图像，并与（a）的结果比较