AI-Lab3
AI-Lab3–搜索算法
任务List
- 利用盲目搜索解决迷宫问题(无需提交)
- 利用启发式搜索解决15-Puzzle问题
- 利用博弈树搜索实现象棋AI(无需提交)
- 利用遗传算法求解TSP问题
任务1:利用盲目搜索解决迷宫问题
尝试利用DFS、BFS、深度受限算法、迭代加深算法、双向搜索算法解决迷宫问题:
- S表示起点;
- E表示终点;
- 1表示墙;
- 0是可通行。
迷宫样例图:
1 | |
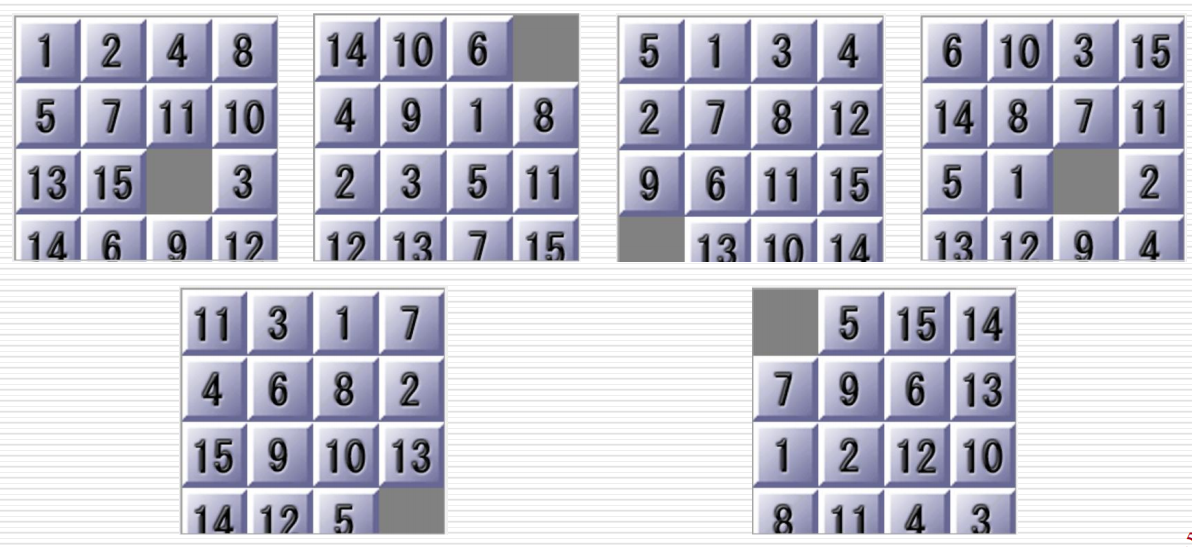
任务2:利用启发式搜索解决15-Puzzle问题
尝试使用A*与IDA*算法解决15-Puzzle问题,启发式函数可以自己选取,最好多尝试几种不同的启发式函数
利用A*算法和IDA*算法解决15-Puzzle问题, 可自定义启发式函数. Puzzle问题的输入数据类型为二维嵌套list, 空位置用 0表示. 输出的解数据类型为 list, 是移动数字方块的次序.
若选择A*算法, 则函数名为 A_star; 若选择IDA*算法, 则函数名为 IDA_star.
例子: 输入
1 | |
则调用 A_star(puzzle)或 IDA_star(puzzle)后输出解
1 | |
相关知识:A*算法的必要知识点:
==算法描述==:
1 | |
==启发式函数:== f(n)=g(n)+h(n)
- f(n)是节点n的综合优先级。(每次选择会选择总和优先级最高,也就是f(n)值最小的节点=>维护一个优先队列)
- g(n)是节点n距离起点的代价
- h(n)是节点n距离终点的预估代价
=>启发函数的选取:(网格形式的图)
- 曼哈顿距离–适用于只允许==上下左右==四个方向移动 √ (同时加上线性冲突判断)
- 对角距离–适用于允许朝八个方向移动
- 欧几里得距离–适用于允许朝任何方向移动
=>计算曼哈顿距离的函数:
1 | |
IDA*算法:IDA*算法是在DFS的基础上,添加启发信息的启发式搜索算法。(IDA * 为采用了迭代加深算法的 A * 算法。)
优点:(相对于A*)
- 不需要判重、不需要排序,利于深度剪枝
- 空间需求减少:每个深度下实际上是一个深度优先搜索,不过有深度限制,使用DFS可以减小空间消耗
缺点:
重复搜索:当深度变大后每次都要从头搜索(不记忆-节省内存)
==算法描述==:
1 | |

算法思路:
Resources:
路径规划之 A* 算法 - 知乎
Solving 15-Puzzle with A* and IDA* | CyberWitch



任务3:利用博弈树搜索实现象棋AI
编写一个中国象棋博弈程序,要求用alpha-beta剪枝算法,可以实现两个AI对弈。
- 一方由人类点击或者AI算法控制。
- 一方由内置规则AI控制。
- 算法支持红黑双方互换
任务4:利用遗传算法求解TSP问题利用遗传算法求解 TSP 问题
- 在National Traveling Salesman Problems(uwaterloo.ca)(https://www.math.uwaterloo.ca/tsp/world/countries.html) 中任选两个TSP问题的数据集。
- 建议:
对于规模较大的TSP问题, 遗传算法可能需要运行几分钟甚至几个小时的时间才能得到一个比较好的结果. 因此建议先用城市数较小的数据集测试算法正确与否, 再用城市数较大的数据集来评估算法性能。
由于遗传算法是基于随机搜索的算法, 只运行一次算法的结果并不能反映算法的性能. 为了更好地分析遗传算法的性能, 应该以不同的初始随机种子或用不同的参数(例如种群数量, 变异概率等)多次运行算法, 这些需要在实验报告中呈现.
resources:
初识Numpy数组,看这一篇就够了! - 知乎
更加详细的要求:
为了方便批改作业, 我们统一用类 GeneticAlgTSP来编写遗传算法的各个模块, 并分析算法性能. 该类需包含以下方法:
- 构造函数
__init__(), 输入为TSP数据集文件名filename, 数据类型str. 例如"dj38.tsp"是Djibouti的38个城市坐标数据文件;"ch71009.tsp"是China的71009个城市坐标数据文件. 我们需要在构造函数中读取该文件中的数据, 存储到类成员self.cities中(数据类型自定, 建议存储为numpy数组). 同时在构造函数中初始化种群, 存储到类成员self.population中(数据类型自定). - 求解方法
iterate(), 输入为算法迭代的轮数num_iterations, 数据类型int. 该方法是基于当前种群self.population进行迭代(不是从头开始), 返回迭代后种群中的一个较优解, 数据类型list, 格式为1-n个城市编号的排列. 例如, 对于n=5的TSP问题, 迭代后返回的较优解形如[1,3,4,5,2], 表示当前较好的游览城市次序为1-3-4-5-2-1.
可以在类中编写其他方法以方便编写并分析遗传算法的性能. 请在代码注释或实验报告中说明每个方法/模块的功能.
steps:
- 读取文件,提取出城市维度和城市坐标
1 | |
- 初始化种族:在城市数较少时使用随机数生成法,中等城市数可以考虑部分贪婪(?,大体量城市再考虑其他
相关资料:NumPy随机排列:使用numpy.random.permutation实现数组元素的随机重排|极客教程
提示
- 数据集来源于网站National Traveling Salesman Problems (uwaterloo.ca). 可浏览该网站参考相关国家的TSP问题的解. 可以自选1-2个数据集来测试算法性能, 并在实验报告中说明.
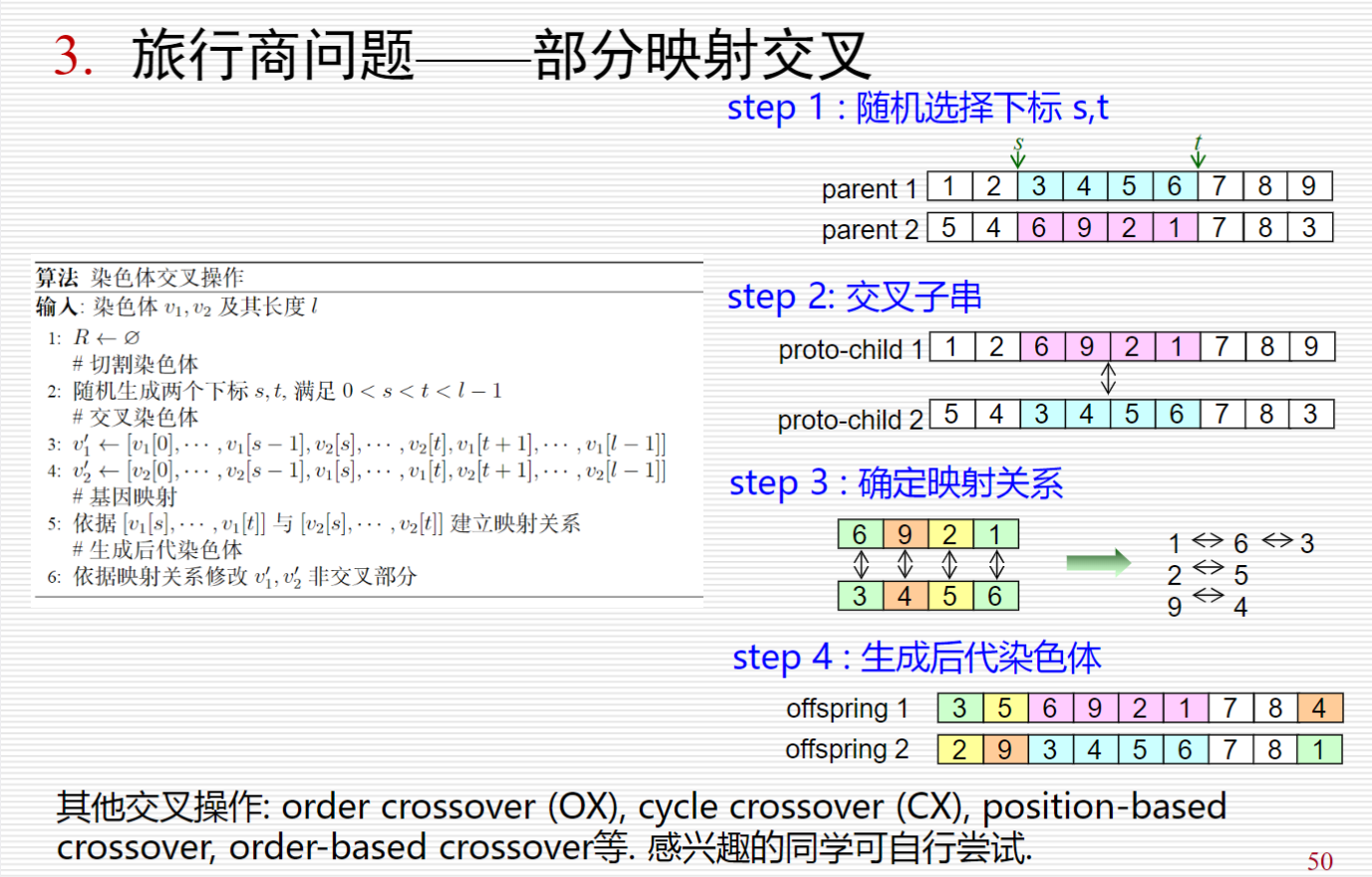
- TSP问题上遗传算法的具体实现(解的表示, 染色体交叉操作等)不一定局限于课件上的方式, 也许存在比课件效果更好的具体实现方法.
- 由于遗传算法是基于随机搜索的算法, 只运行一次算法的结果并不能反映算法的性能. 为了更好地分析遗传算法的性能, 应该以不同的初始随机种子或用不同的参数(例如种群数量, 变异概率等)多次运行算法, 这些需要在实验报告中呈现.
- 最后提交的代码只需包含性能最好的实现方法和参数设置. 只需提交一个代码文件, 请不要提交其他文件.
- 对于规模较大的TSP问题, 遗传算法可能需要运行几分钟甚至几个小时的时间才能得到一个比较好的结果. 因此建议先用城市数较小的数据集测试算法正确与否, 再用城市数较大的数据集来评估算法性能.
- 本次作业可以使用
numpy库以及python标准库. 有余力的同学可用matplotlib库对遗传算法的结果进行可视化处理与分析, 并在实验报告中呈现.
高级搜索
模拟退火算法
简介
模拟退火算法SA来源于固体退火原理,是一种基于概率的算法。
模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,==结合概率突跳特性在解空间中随机寻找目标函数的全局最优解==,即在局部最优解能概率性地跳出并最终趋于全局最优。
[!NOTE]
算法思想为:先从一个较高的初始温度出发,逐渐降低温度,直到温度降低到满足热平衡条件为止。在每个温度下,进行n轮搜索,每轮搜索时对旧解添加随机扰动生成新解,并按一定规则接受新解。
原理
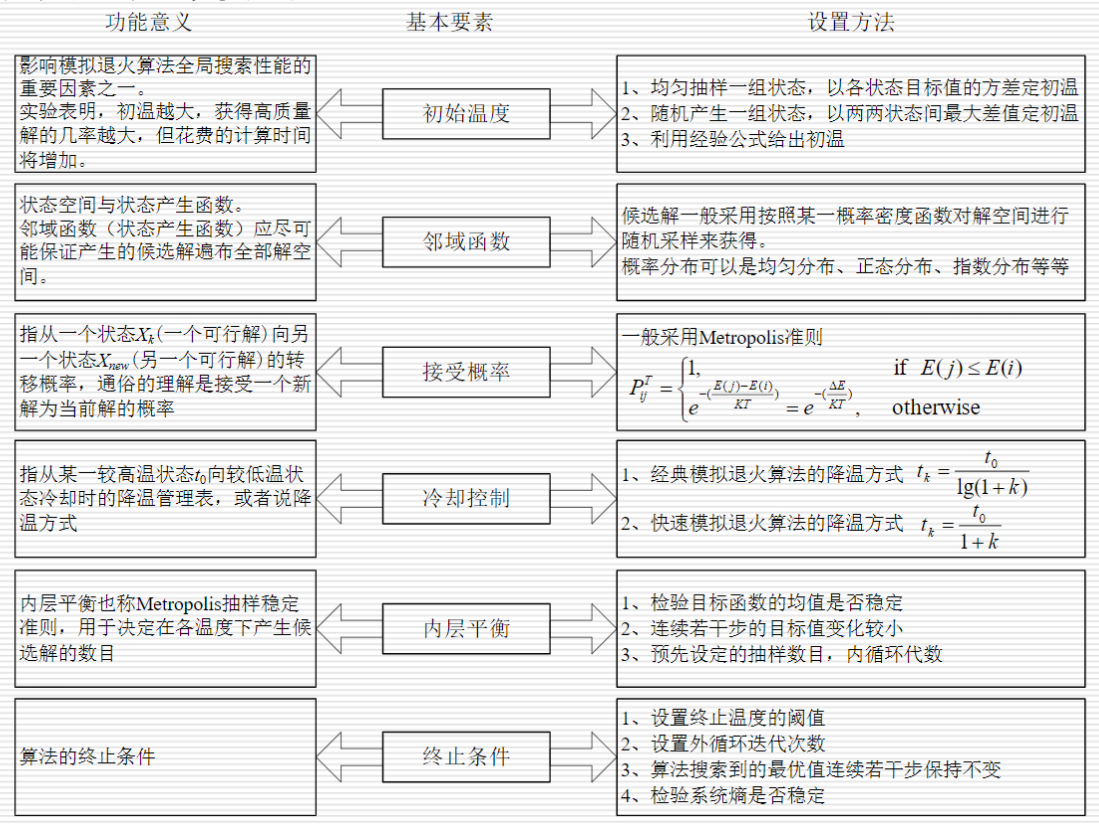
模拟退火算法包含两个部分即==Metropolis算法==和==退火过程==,分别对应内循环和外循环。
- 外循环就是退火过程,将固体达到较高的温度(初始温度T(0)),然后按照降温系数alpha使温度按照一定的比例下降,当达到终止温度Tf时,冷却结束,即退火过程结束。
[!NOTE]
外层循环控制温度由高向低变化
内层循环中温度固定,对旧解添加随机扰动得到新解,并按一定规则接受新解。迭代次数成为马尔可夫链长度
- Metropolis算法是内循环,即在每次温度下,迭代L次,寻找在该温度下能量的最小值(即最优解)。
算法优点
不管函数形式多复杂,模拟退火算法更有可能找到全局最优解。
过程图:
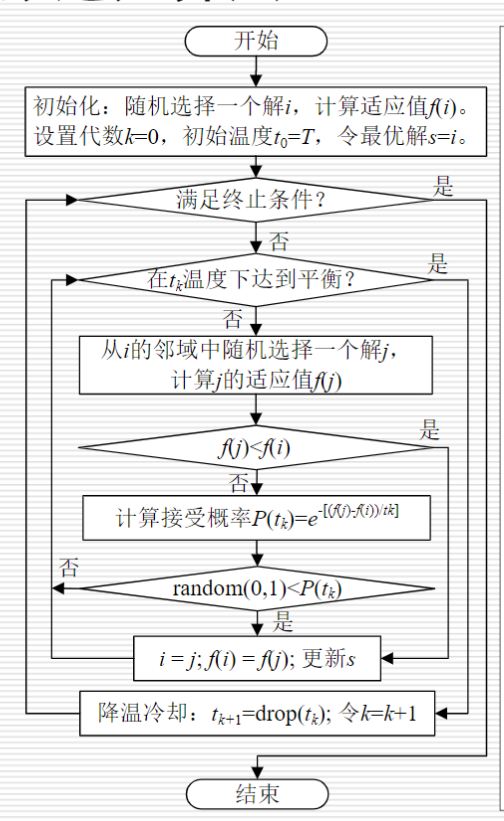
伪代码:
resources:
模拟退火算法超详细教程 - 知乎
遗传算法
[!NOTE]
遗传算法是受自然进化理论启发的一系列搜索算法。
达尔文进化论的原理概括总结如下:
- ==变异==:种群中单个样本的特征(性状,属性)可能会有所不同,这导致了样本彼此之间有一定程度的差异
- ==遗传==:某些特征可以遗传给其后代。导致后代与双亲样本具有一定程度的相似性
- ==选择==:种群通常在给定的环境中争夺资源。更适应环境的个体在生存方面更具优势,因此会产生更多的后代
进化算法:
- 选择
- 交叉(或重组)
- 变异
达尔文进化论<=>遗传算法的对应概念
- 遗传算法试图找问题的最优解
| 达尔文进化论 | 遗传算法 |
|---|---|
| 保留种群的个体性状 | 保留了针对给定问题的候选解集合 |
| 适者生存并更有可能遗传优良特性 | 候选解经过迭代评估,越优的解越有可能将特征传递给下一代候选解集合 |
算法的基本思想:
在求解问题时从多个解开始,然后通过一定的法则进行逐步迭代以产生新的解
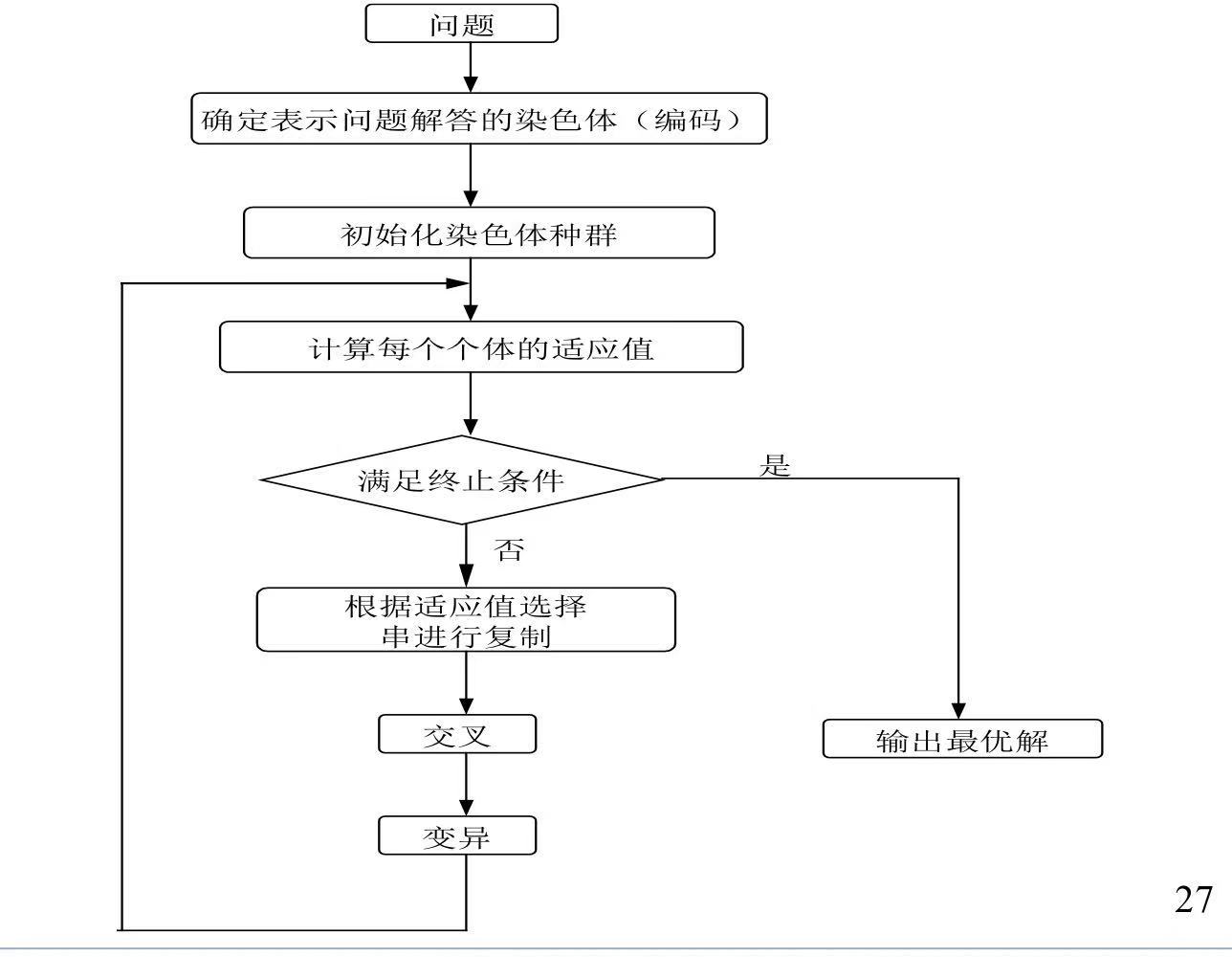
遗传算法的过程:
- 开始时,种群随机初始化,并计算每个个体的适应度函数,初代产生
- 如果不满足优化准则,开始产生新一代计算
- 为了产生下一代,按照适应度选择个体,父代进行基因重组而产生子代
- 子代有几率变异,子代的适应度被重新计算
- 循环直到满足优化准则
伪代码:
resources:
遗传算法 (Genetic Algorithm, GA) 详解与实现 - 知乎
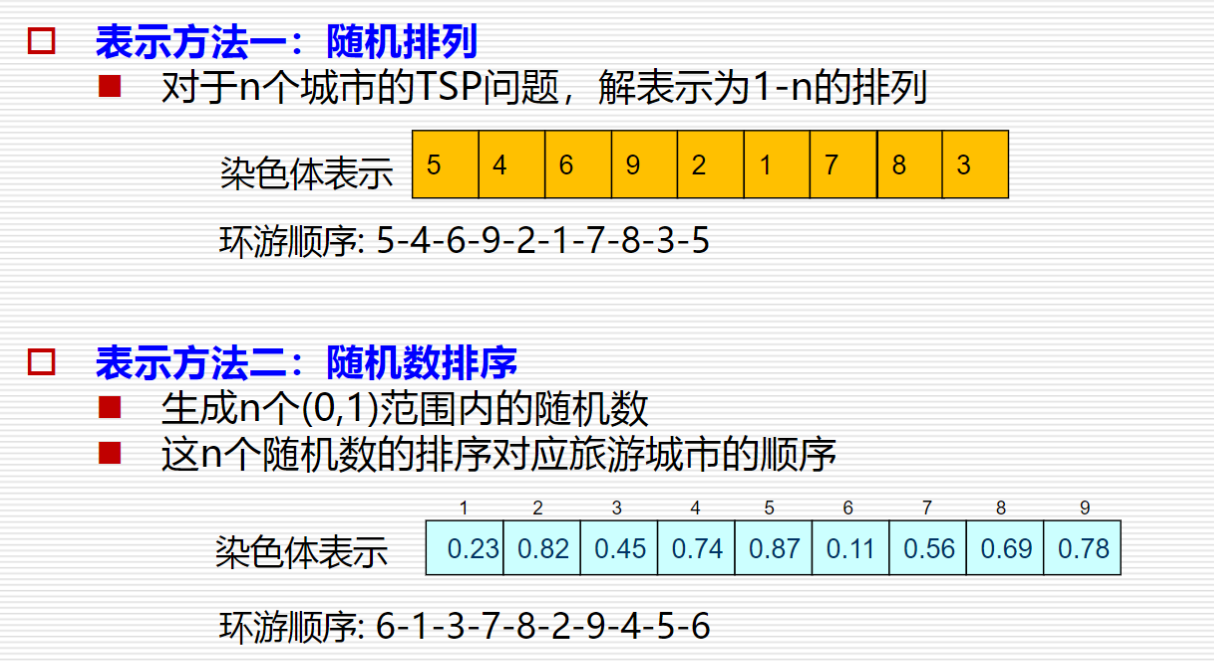
旅行商问题–解的表示