AI-Lab3

基础知识

监督学习与无监督学习

监督学习

• 训练集有标签y
• 目标是找到能区分正负样本的决策边界，据此拟合一个假设函数
• 分类问题

无监督学习

• 训练集的数据不带有标签y
• 需要根据样本间的相似性对样本集进行聚类，试图使类内差距最小化，类间差距最大化
• 聚类问题
  • k-means，密度聚类，层次聚类等

K聚类

算法概述：

• K-means算法是一种无监督学习方法。
• 使用一个没有标签的数据集，然后将数据聚类成不同的组。
• 通过迭代将数据点分配到K个簇中，使得每个数据点与其所属簇的中心(质心)之间的距离平方和最小化。

距离度量：

• 闵可夫斯基距离（Minkowski distance）
  • p=2–欧式距离
  • p=1–曼哈顿距离
  • 切比雪夫距离

算法流程：

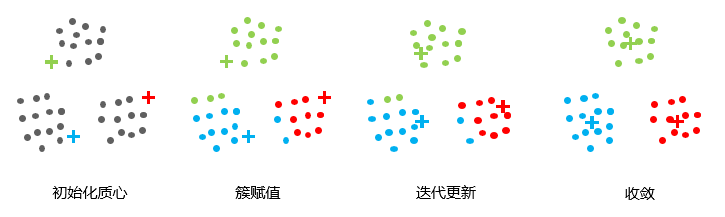
1. 选择K个点作为初始质心。（初始化簇质心为任意点）
2. 将每个点指派到最近的质心， 形成K个簇。（遍历所有数据点，计算所有质心与数据点的距离，根据距离选择簇）
3. 对于上一步聚类的结果， 对所有簇计算平均距离， 得出该簇的新的聚类中心（新的质心）。
4. 重复上述两步/直到迭代结束：质心不发生变化。
   

优点

• 原理简单，实现容易，收敛速度快
• 聚类效果较优
• 算法的可解释度比较强
• 主要需要调参的参数仅仅时簇数K

缺点
◼ 需要预先指定簇的数量
◼ 无法区分高度重叠的数据
◼ 欧几里得距离限制了能处理的数据变量类型
◼ 随机选择质心并不能带来理想的结果
◼ 无法处理异常值和噪声数据
◼ 不适用于非线性数据
◼ 对特征尺度敏感
◼ 如果遇到非常大的数据集，计算机可能会崩溃

实验任务

聚类任务

• 在给定数据集上，设计合适的k以及距离度量函数，利用k-means算法完成数据的聚类
• 要求：
  • 尝试分别在前200条、前1000条、前10000条数据完成聚类。
  • 画出聚类后的数据可视化图。

聚类个数K和初始聚类中心的选取

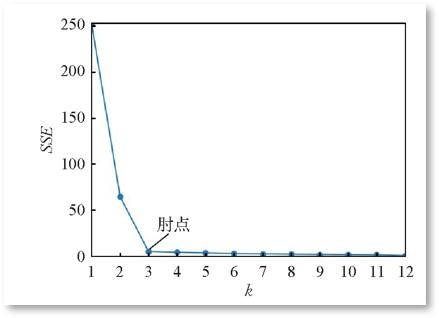
• 合适的k值怎么选取？=>手肘法
• 聚类的目标是使得每个样本点到距离其最近的聚类中心的总误差平方和（也即聚类的代价函数–SSE）尽可能小
  $$
  SSE=\sum\limits_{i=1}\limits^k\sum\limits_{x\in{C_i}}|d(x,C_i)|^2

$$
SSE的大小表示聚类结果的好坏，k为簇的个数
$d(x,C_i)$表示的是欧拉距离公式

方法二：Gap Statistics方法（自动）
$Gap(K)=E(logD_k)-logD_k$
$D_k$为损失函数，$E(logD_k)$是期望。
这个数值通常通过蒙特卡洛模拟产生，我们在样本里所在的区域中按照均匀分布随机产生和原始样本数一样多的随机样本，并对这个随机样本做 K-Means，从而得到一个$D_k$ 。如此往复多次，通常 20 次，我们可以得到 20 个$logD_k$  。对这 20 个数值求平均值，就得到了$E(logD_k)$ ​ 的近似值。最终可以计算 Gap Statisitc。而 Gap statistic 取得最大值所对应的 K 就是最佳的 K。

初始聚类中心：

• 对初始聚类中心的位置敏感
• 优化方式：
  • 最大距离法（课上学过）
    • 先选取数据集中距离最大的两个点作为初始聚类中心
    • 将剩余数据对象进行分配，更新聚类中心
    • 继续寻找与聚类中心距离最远的点作为下一个中心点

资料：

最常用的聚类算法——K-Means原理详解和实操应用(R&Python) - 知乎