AI-Lab4.2

人工神经网络介绍

单层感知机

  • 由于M-P神经元模型参数需要事先设定好，为了能够自适应学习出所需要的参数，研究人员就提出了单层感知机(Perceptron)
  • 感知机的基本公式为：y(𝑥)=𝑠𝑖𝑔𝑛(𝑤𝑥+𝑏)
  • sign为符号函数，当自变量为正数时取值为1，否则取值为0

多层感知机

  • 包含三个层次：一个输入层，一个或多个中间层(也叫隐藏层，hidden layer) 和一个输出层
  • 输入层与输出层的节点数是固定的，中间层则可以自由指定
  • MLP通常还会引入偏置单元b

激活函数

  • 常见：sigmoid、Relu、tanh
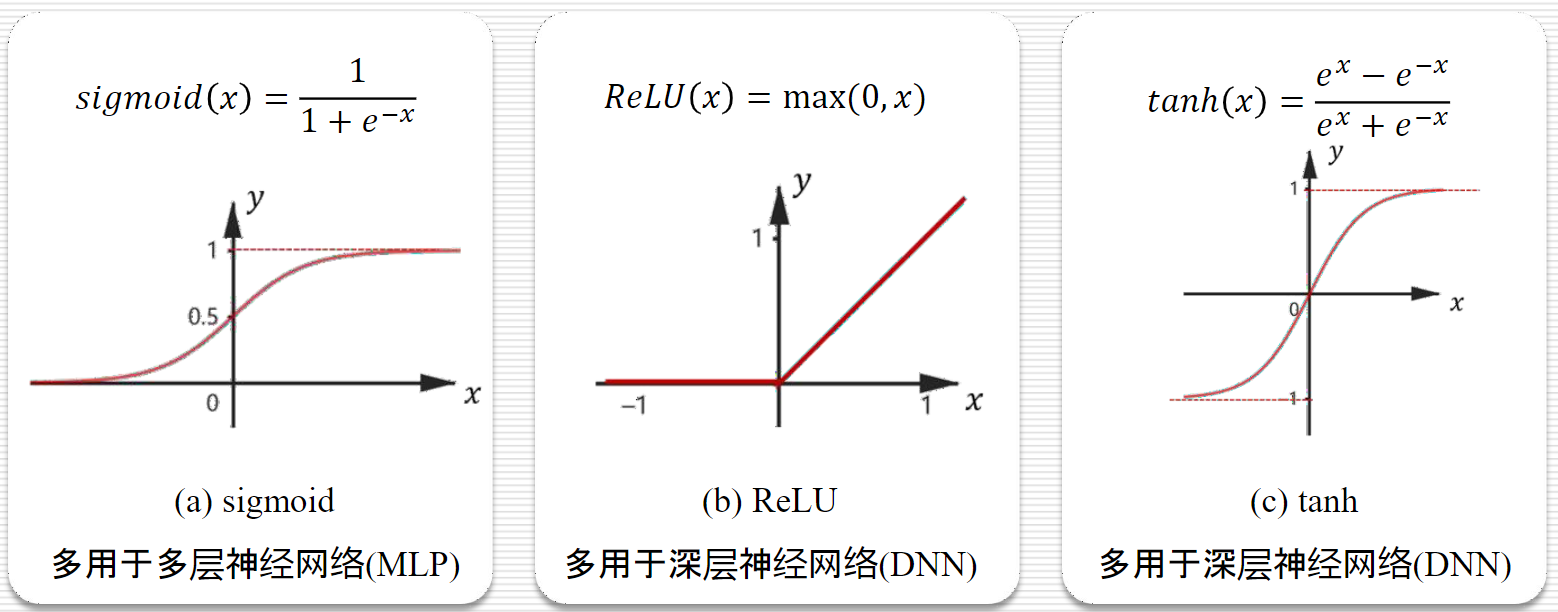
  • sigmoid可以用于计算概率
  • ReLU函数的拟合效果可能更好一点
  • tanh函数

损失函数

  • 作用：衡量网络表现是否良好，并为之后的网络参数优化提供指导

梯度下降

  • 梯度定义：梯度是一个向量，表示某一函数在该点出的方向导数沿着该方向取得最大值。
  • 梯度下降的一般公式为：𝜃=𝜃−𝜂∇𝜃𝐿(𝜃)，其中，𝜂是学习率，∇𝜃是对𝜃的梯度，𝜃是参数
    • 学习率太小学习地很慢
    • 学习率太大效果不太好，可能错过最小值，无法收敛

作业

2.1：购房预测分类任务

  • 利用感知机算法在给定数据集完成购房预测训练
  • 要求：
    • 选择合适的损失函数，利用训练集完成网络训练，画出数据可视化图、loss曲线图。（可以任意拿两个特征、三个出来画，全部都要画出来）
    • 单层感知机示例：

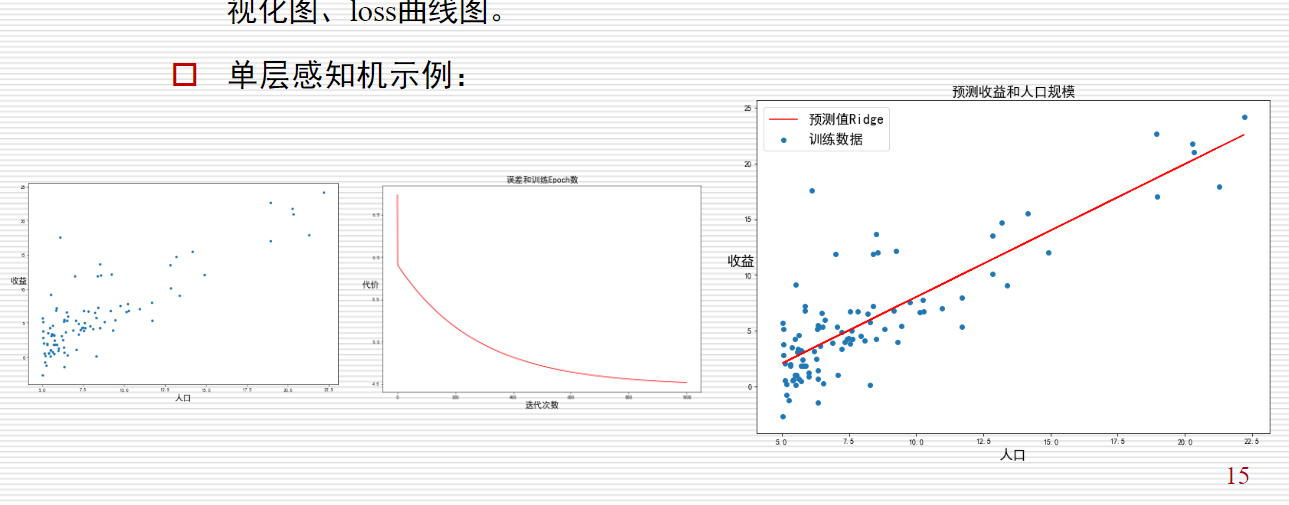
=>感知机算法

房价预测任务

data.csv数据集包含五个属性，共10000条数据，其中 longitude和 latitude表示房子经纬度，housing_age表示房子年龄，homeowner_income表示房主的收入（单位：十万元）， house_price表示房子的价格。请根据数据集 data.csv中四个属性 longitude、latitude、housing_age、homeowner_income，利用感知机算法预测房价 house_price，并画出数据可视化图、loss曲线图。

提示

  1. 最后提交的代码只需包含性能最好的实现方法和参数设置. 只需提交一个代码文件, 请不要提交其他文件.
  2. 本次作业可以使用 numpy库、matplotlib库以及python标准库.
  3. 数据集可以在Github上下载。

实现过程：

整体流程：

1.1 数据处理
  • 加载数据集、数据预处理（标准化/归一化）
  • 划分训练集和测试集（8:2）

=>利用 loadtxt函数读取csv文件:

1
2
3
4
5
6
7
8
9
np.loadtxt(filepath,delimiter,usecols,unpack)

'''
参数：
filepath:加载文件路径  
delimiter:加载文件分隔符  (csv一般以','进行分隔)
usecols:加载数据文件中列索引（标签）
unpack:当加载多列数据时是否需要将数据列进行解耦赋值给不同的变量 
'''
1.2 感知机模型构建
  • 定义感知机模型结构（__init__，参数包括：学习率，迭代次数，loss数组)
  • 实现前向传播算法
  • 实现反向传播与权重更新
1.3 模型训练与评估
  • 设定超参数（学习率、迭代次数等）
  • 训练模型并记录loss
  • 在测试集上评估模型性能
1.4 可视化结果
  • 数据分布可视化
  • loss曲线绘制

知识补给：

感知机概述：

  • 感知机是二分类的线性分类模型，属于监督学习算法（提供label进行训练）
  • 为求得超平面，感知机导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化求解。
  • 如果训练数据集是线性可分的，则感知机一定能求得分离超平面。如果是非线性可分的数据，则无法获得超平面。

感知机模型

感知机模型：$f(x)=sign(w⋅x+b)$

  • sign()是符号函数
  • 其中的一个超平面是$wx+b=0$

感知机损失函数（loss）

损失函数的一个自然选择是误分类点的总数，但是这样的函数不是连续可导函数，不易优化。因此感知机采用的损失函数是误分类点到超平面的总距离。

对于误分类样本 $(x_i, y_i)$（满足 $y_i(w \cdot x_i + b) \leq 0$），损失函数为误分类点到超平面的距离的相反数：

$$
L(w,b) = -\sum_{x_i \in M} y_i(w \cdot x_i + b)
$$

其中 $M$ 是误分类样本集合。

距离公式推导

误分类点到超平面的几何距离：$||w||$是w的$L_2$范数

$$
\text{Distance} = \frac{|w \cdot x_i + b|}{|w|_2}
$$

因误分类时 $y_i(w \cdot x_i + b) < 0$，可简化为：

$$
\text{Distance} = -\frac{y_i(w \cdot x_i + b)}{|w|_2}
$$

梯度下降更新规则

参数更新公式（$\eta$ 为学习率）：

$$
\begin{aligned}
w &\leftarrow w + \eta y_i x_i \
b &\leftarrow b + \eta y_i
\end{aligned}
$$

梯度计算：

$$
\begin{aligned}
\nabla_w L &= -y_i x_i \
\nabla_b L &= -y_i
\end{aligned}
$$

收敛性定理（Novikoff）

对于线性可分数据集，感知机保证在有限步 $k$ 内收敛：

$$
k \leq \left( \frac{R}{\gamma} \right)^2
$$

其中：

  • $R = \max |x_i|$ 是输入特征的最大模长
  • $\gamma$ 是分离超平面的间隔（margin）

多层感知机：

  • 要手写权重、偏置、梯度下降率
学习笔记 > AI
#AI #学习笔记
AI-Lab4.2
https://pqcu77.github.io/2025/04/21/AI-Lab4-2/
作者
linqt
发布于
2025年4月21日
许可协议